Polígonos de Thiessen ou Voronoi- Como gerar e para que utilizá-los

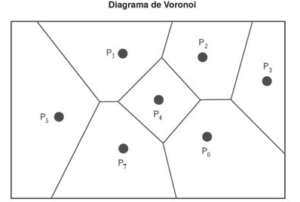
Conceito

Polígonos de Thiessen ou diagramas de Voronoi, que na prática são nomes diferentes para a mesma coisa,  nada mais é do que um conjunto associado de regiões em torno de pontos no plano euclidiano.

Mas não é qualquer região ou área, mas sim as que estão mais próximos de um dos pontos do que de qualquer outro ponto. Estas regiões são conhecidas também como polígonos de proximidade, polígonos de Voronoi ou regiões de Thiessen.

Uso

• Uma das primeiras aplicações do Diagrama de Voronoi foi feito por John Snow para estudar a epidemia de cólera no bairro londrino do Soho em 1854, localizado na Inglaterra. Ele mostrou a correlação entre áreas do mapa de Londres e as áreas com mais mortes devido ao surto, utilizando uma bomba de água particular.
• Encontrar um hospital mais próximo ou o objeto mais similar em um banco de dados. Uma aplicação importante é a quantização vetorial, comumente utilizada em compressão de dados.
• Com um determinado Diagrama de Voronoi pode-se também encontrar o maior círculo vazio dentre um conjunto de pontos em um polígono abrangente; por exemplo, para construir um novo supermercado o mais distante possível dos demais supermercados existentes, em uma determinada cidade plana.
• Diagrama de Voronoi é útil em física de polímeros. Pode ser utilizado na representação do volume livre do polímero. Também é utilizado em derivações da capacidade de uma rede sem fio.
• Em Climatologia, Diagramas de Voronoi são utilizados para calcular a precipitação de uma área, com base em uma série de medições pontuais. Neste caso, geralmente referenciados como polígonos Thiessen.
• Diagramas de Voronoi são utilizados para estudar os padrões de crescimento das florestas. Também pode ser útil no desenvolvimento de modelos preditivos para incêndios florestais.
• Diagramas de Voronoi também são utilizados em computação gráfica para gerar alguns tipos de texturas orgânicas.
• Em robótica autônoma de navegação, Diagramas de Voronoi são utilizados para encontrar rotas livres. Se cada obstáculo do percurso for representado por um ponto, então as bordas do diagrama serão as rotas mais distantes dos obstáculos (afastando assim, em teoria, o risco de colisões).
• Em química computacional, as células Voronoi definidas pelas posições dos núcleos em uma molécula são usadas para calcular cargas atômicas. Isto é feito utilizando o método de densidade de deformação de Voronoi.
• Na ciência dos materiais, microestruturas policristalinas em ligas metálicas são geralmente representadas utilizando Diagramas de Voronoi.
• Polígonos de Voronoi têm sido utilizados na mineração, para estimas as reservas de materiais valiosos, minerais e outros recursos. Os pontos onde já ocorre a exploração são utilizados como o conjunto de pontos nos polígonos de Voronoi. (by Wikipedia)

No ArcGIS

Disponível na versão advanced, a ferramenta chama-se “Create Thiessen Polygons” disponível na Analysis toolbox>Proximity toolset. Ela toma como entrada um arquivo de pontos e como saída gera um arquivo de polígonos.

O algoritmo elabora a triangulação e gera os polígonos contendo apenas um ponto por célula Thiessen. Cada célula corresponde a área de influência máxima daquele ponto na amostra no plano.

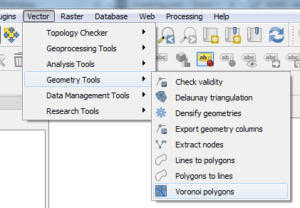
No QGIS

Naturalmente o QGIS também possui a mesma ferramenta. Porém o chama de “Voronoi Polygons” no menu Vector>Geometry Tools.

Da mesma forma que o ArcGIS, no QGIS este algoritmo toma uma camada de pontos e gera uma camada de polígono contendo os polígonos voronoi correspondentes aos pontos de entrada.

Na próxima vez que precisar analisar a área de influência de um evento pontual, não deixe de considerar os polígonos de Thiessen ou Voronoi na suas análises.